> ○○の解釈 > その5 実数とは何か?
> ○○の解釈 > その5 実数とは何か?

その5 実数とは何か?(掲載日 2021.01.29)
実数とは何でしょう?

実数は直線に結びついた数で、
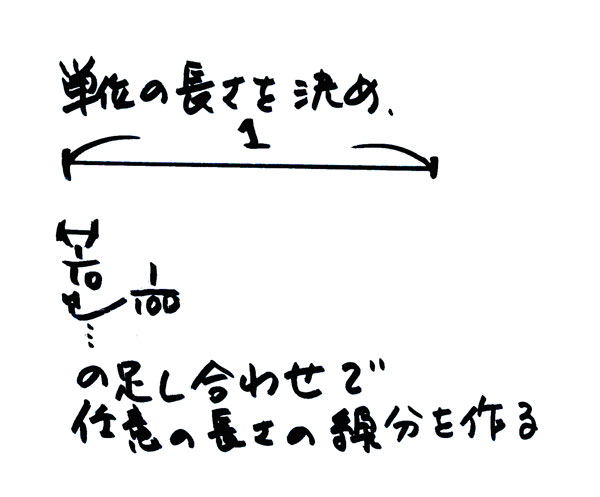
ある長さを単位の長さ1と決めて、
全ての2点間の距離を単位の長さとの比(単位の長さの何倍か)で
数値化した(数字化した)数
と言えるのではないでしょうか?
普段使っている数直線と同じイメージなのですが、
ここでは数を表す道具として使っていました。
数直線はただの道具だったのではなく、
実数は直線から生まれるよう
です。
しっかり確認してみましょう。
(基本的には数直線を利用していた感覚通りのようです。)
数値化(数字化)するとは
134.5555500000・・・
のように表したり、
のように
概念で大きさを表したりした数
にすることです。
134.5555500000・・・
については
10進数の数である場合、
単位の長さの線分(つまり、長さ1)を134個始点と終点を繋いで同じ向きにまっすぐに並べ、
単位の長さの線分の10分の1の長さの線分を5個、
単位の長さの線分の100分の1の長さの線分を5個、
単位の長さの線分の1000分の1の長さの線分を5個、
単位の長さの線分の10000分の1の長さの線分を5個、
単位の長さの線分の100000分の1の長さの線分を5個
同様に並べることで
表現することができます。
<数値化(数字化)するときの方法>
単位の長さの線分、10分の1の線分など基準の線分を継ぎ合わせて長さを作るのですが、
数値化したい長さの点を超すまで、
単位の長さの線分を伸ばし、
超えたら、その下の位の長さの線分を足して伸ばしていく方法で
任意の数字を作れる(興味のある長さを測れる)でしょう。
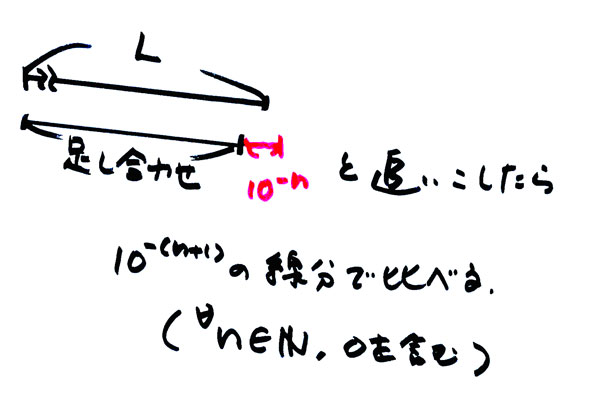
(nは任意の自然数。 nが全ての自然数で成り立つ。)
ぴったり「いくら」と言える場合には
例えば、134.55550000・・・・のように
小数点以下のある位以下の数字が全て0となるのですが、
単位の長さの線分の100000分の1の長さの線分など、基準となる線分を足して継ぎ合わせると
ぴったりの位置に来た場合となり、
小数点以下の数字がどこまで行っても0000・・・とならない場合は
永遠に基準となる線分を足して継ぎ足していくことになります。
<数の大小と距離の大小>
直線を用いて実数を表す方法において、
大小関係を考えると、
7.5は7.7よりも
単位の長さの線分の10分の1の長さの線分が2個分足りないので、
7.5は7.7よりも小さい大きさの数
と言えます。
実数全体を表すには
原点から反対方向に伸びる2本の半直線
(つまり、どこかに原点が1つ乗っている1本の直線)
が必要となります。
なぜなら、
実数は任意の点と点間の距離
(2点を結ぶと直線になります。)
で表すことができ、
実数全体は「穴のない直線」で表されないと
表すことのできない数が存在することになります。
数直線上の任意の実数は
原点から伸びる直線上の任意の点と原点間の距離
(負の領域は原点からの距離にマイナスを付けた数)
で
表すことができ、
先ほどの、数の大小と距離の大小の関係より、
絶対値の小さい数字の方が原点に近くなり、
大小で一意に並べることができるので、
数直線で考えたほうが議論がすっきりするかもしれません。
(始点を原点と考えたほうが絵の想像がしやすいでしょう。
逆に、原点を任意の始点と変えて考えることはできます。)
ここで一つ考えたほうが良いことがあります。
「実数の集合」を
「0,2,3.44,・・・」などと
数1つ1つの集合体として
数え上げることができるでしょうか?
実数1つに対して、数直線上の点1つが該当します。
なぜなら、数値化した時に、1通りにしか長さのパーツの組み合わせがないからです。
そのため、始点(原点)から長さのパーツを加え合わせたときに到達する場所は1か所しかありません。
逆に、数直線上の全ての点は1つの実数が該当します。
(先ほどの数字化するときの方法で、一つに決めることができますので。)
実数を1つ1つ数え上げて、
実数全体の集合を表す行為は
点を並べて、何らかの集合体を作ろうとする行為で、
ここでは、点を並べて1本の直線を作ろうとする行為です。
しかし、
幅0の点をいくら並べても(無限個並べても)、
長さのある直線(幅のある物体)にはなりません。
(「○○の解釈」 「その4 直線を並べると面になるか」 参照ください。)
ですから、
「全ての実数の間に実数が存在する」という証明では
(例えば、任意の数、a、bの間に数が存在するので、
どんなに近いと考えられる2数の間にも数は存在する。)
実数の連続は
証明できません。
実際、
有理数に関して、同様に
「全ての有理数の間に有理数は存在する」と証明されますが、
(例えば、任意の数、a、bの間に数が存在するので、
どんなに近いと考えられる2つの有理数の間にも数は存在する。)
有理数は連続ではありませんでした。
(「○○の解釈」 「その4 有理数、無理数の 連続」 参照ください。
ここでは、縦横1の正方形の面積を求めるときに直線を使っているので、連続が保証されています。)
なので、
「全ての実数の間に実数が存在する」という証明では
きちんと連続であることを議論で追うことができていない可能性があります。
逆に、
直線からある1点を選ぶことはできますので、
ある数字を言うと、実数であると言えるでしょう。
数直線上に対応する長さの点が存在すれば、
その数は実数と言えるはずですから。
数は全て、比例の比としても存在できますので、
必ず対応する長さはありますので。
また、無限遠の2点(数直線では直線の端)が無限大に相当し、
などの概念で表した数は
始点から数えてその大きさの位置に点が来ます。
例えば、
面積2の正方形の一辺の長さがを表し、
数直線上では
面積2の正方形の頂点の1点を原点において、
1辺を数直線上の正の部分に乗せれば、
数直線上の原点以外の頂点は
の位置にある
などして、
長さを示すことができます。
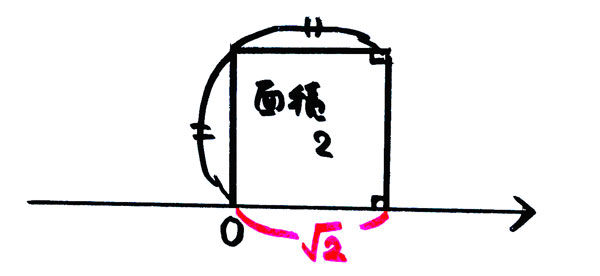
(2の19乗根は、19回かけて2になる数の位置に点が来ます。
面積の数値化は
単位長さの正方形の面積を単位の面積として1、
それを基に10分の1などとして、
敷き詰めればできるでしょう。
体積も同様です。)
以上より、
先ほどの、数の大小と距離の大小の関係より、
絶対値の小さい数字の方が原点に近くなり、
大小で一意に並べることができるので、
数直線を使うことで、
全実数を数え上げる(示す)ことができます。
今までの数直線の使い方は
線を引いて、ある点を1として、2などの数字を選んで示していたので、
直線上の点をピックアップする方法だったので、
問題ない感じのよう
です。
以上のように
実数の集合は直線であると考えられそうなので、
そういうイメージで良いのではないでしょうか?
(数が存在するという方向性の証明の仕方では
実数の連続性は出て来ない感じで、
そもそも直線上の点として考えるほうが自然なよう
なんですよ。)
この数値化(数字化)は
n進数(nは2以上の全ての自然数、10進数で表すことが普通)で行うこともできて、
10進数として表した実数の集合としてだけでなく、
3進数でも7進数でも16進数でも表すことができるので、
つまり、同じ長さの線分の数字化した時の表記が違うだけなので、
直線はn進数で表した実数空間(集合)を表すことができます。
ちなみに、
具体的な数字化の方法は
例えば3進数の時は3分の1の長さの線分で小数点第1位の数の長さ、
9分の1の長さの線分で小数点第2位の数を表せば良いです。
(それ以下は同様に累乗した長さを基準とします。)
この場合、概念を表した数は進数を変えても、
特に位置を変えません。
10進数でも3進数でも
の位置は変わりませんし、
10進数での位置は
3進数でと表されるだけで、
同じ場所です。
結論として、
「実数は直線的に連続」で、
「その中身は不連続な有理数とその間を埋める連続な無理数でできている」
という結論です。
(「実数」は、「有理数」と「有理数ではない数、つまり無理数」でできています。
「○○の解釈」 「その4 有理数、無理数の 連続」 参照ください。)
P.S. この記事では実数の姿について、交通整理してみました。
<修正>2021.01.29
「以上のように
実数の集合は直線であると考えられそうなので、
そういうイメージで良いのではないでしょうか?
(数が存在するという方向性の証明の仕方では
実数の連続性は出て来ない感じで、
そもそも直線上の点として考えるほうが自然なよう
なんですよ。)」
のように、
「実数の連続性」という言葉に直しました。
<追加>2021.01.29
<本文>のP.S.の前に
結論を付け加えました。
ブログ「考えてみたら、こーなった」の
「1268. 「実数の連続性」について考えてみたよ」に
感想などなどが書いてあります。


 > ○○の解釈 > その5 実数とは何か?
> ○○の解釈 > その5 実数とは何か?





 > ○○の解釈 > その5 実数とは何か?
> ○○の解釈 > その5 実数とは何か?