> ○○の解釈 > その７ 「量化する」との付き合い方
その７ 「量化する」との付き合い方（掲載日 2020.02.14）
僕たちは
どれくらいの量の物があるのか、
どれくらいの長さなのか、重さなのか知るために、
単位となる大きさを決めて、
「数字化」することで
大きさのイメージを図ってきました。
その道具は物差しやメスシリンダーなどです。
（重さは、バネの長さや水に浮かべたときの体積などで測ると思いますが、省きます。）
小学校の理科や算数の授業で読み方を習い、
物差しやメスシリンダー、温度計の使い方を学びました。
これらのものには
目盛りが書いてあって、
最小目盛りの１０分の１まで目分量で数字を決めて、
数字化するように言われています。
しかし、
そもそもこの世にある大きさ、例えば、線分の長さは
「○○の解釈」「その５ 実数とは何か？」で考えたように
必ずしも、ピッタリの数字になるとは限りません。
数字化すると最小目盛りの大きさに相応した誤差が出ることになります。
数字化した数（数学の神様的な数ではなく、人間の数）には
誤差がつきもの
となります。
「ここまでは正しいよ」という有効数字を気にして
数字を扱わねばなりません。
（「根本の根」高校生編「17.有効数字って何？」参照ください。）
物を作るとき、
「ちょうどいい大きさ」が必要な場合があります。
「ちょうどいい大きさ」というのは
「○○して、△△したら、出てきた長さピッタリの大きさ」だったりして、
「２辺の長さを決めて作った直角三角形の残りの辺の長さ」ですら、
僕たちの使っている定規にとっての
ぴったりの数字になることはほとんどなく、
誤差のない数字にすることができません。
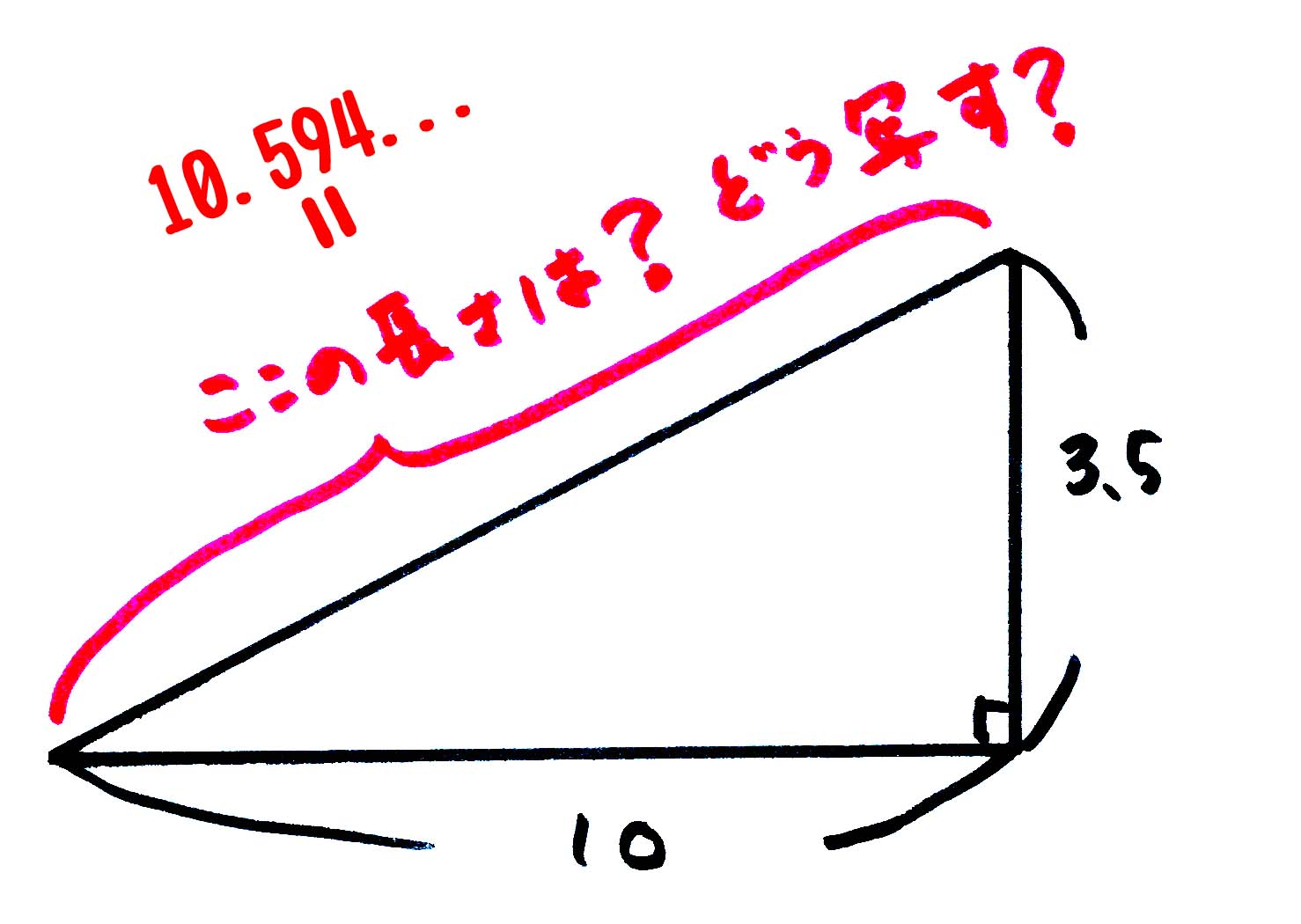
つまり、
同じ大きさの線を別の場所に引いて、長さを再現しようとしても、
物差しで測った数字を持って、別の場所に移動すると
誤差を含んで移動することになり、
理論的な時点で、再現できない
のです。
この場合、
少なくとも長さを移動させるのにかかる時間中は
ゆがまない、伸びたり縮んだりしない材質のものに
長さ自体を写して、長さの目盛りの描かれた（始点、終点の描かれた）そのもの自体を持って、
つまり、線分自体を持って、
場所を移動させないと
ピッタリの長さで線分を再現することができません。
例えば、木造家屋、木造建築を作る場合や家具を作る場合、
出来上がりにおける
許される誤差が定規の目盛りの１００分の１以下だったりするので、
線分の長さの情報を数字にして、
別の場所に運ぶことでは誤差が大きすぎて
物の用をなさない
でしょう。
ハンドメイドでやるしかないんです。
手でやっているからと言って、
大工さんの用いている規矩術（きくじゅつ）は
原始的な技術ではなく、
必要な精度を出すための「本物」の技術のようです。
「大きさをこれくらいにしよう」と
人間が仕組んだ長さ（直角三角形の２辺の長さ）を指定するのにのみ
定規は使えて、
残りの発生した長さは
うつすしかないようです。
（別の場所に、同じ直角三角形を作っても良いですが。）
測れない長さを等分したり、何倍かにするのはどうすれば良いか
というと
三角形の相似を使って、平行線を用いれば
数字化しなくても作図によって、
欲しい長さの線分を手に入れることができます。
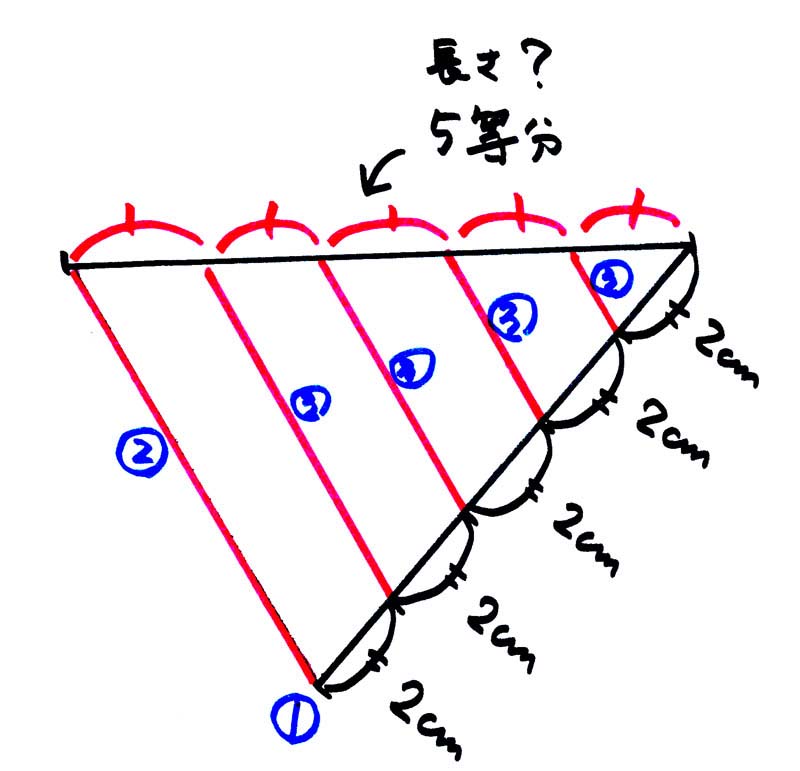
（１．まず、仕組んだ長さで５等分を作る。
２．端のラインを出す。
３．端のラインに平行に線を引いた足が知らない長さの線分の５等分の点。
中学での幾何が作図の基本のようです。
また、そもそも、物差しに「よく使うピッタリの長さでない目盛り」を入れてあるのは
長さ自体を運んでいるので、考えられているなと思います。
例えば、を基本とした目盛りや
欲しい長さの円の直径を示す目盛りなど）
立体的に斜めの線分を
正面図や側面図、平面図などにすると
必ず長さが変わります。
それは、
直角三角形的に相似な図を用いて表されますが、
ここでも、
作図によって数字化せずとも
きっちりとした長さを出すことができます。
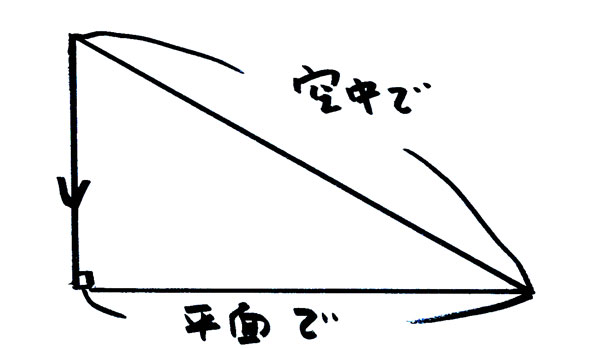
逆に
平面図などの射影図から実際の立体を作ることもできるよう
です。
また、
形を移す場合、
形は任意の２点間の長さが保たれれば、
同じ形となりますので、
長さそのものを移動させれば有効なのですが、
型紙などの型を作って、移すのは有効でしょう。
（最終的にはカンナなどで削り出すようですが。）
人類は
量化することで、
大体の大きさの程度を知ることができるようになり、
この量を比較することで
自然科学が大発達しました。
大体の大きさを実感するのは僕たちにとって非常に有用ですし、
大きさにしないと、
寄与の重要性など比較できないものもあります。
（「80. 箇条書きと数値化による比較」参照ください。）
また、
実測に基づく、いくつかの量の間の関係式も出すことができません。
（対比として、面積や体積を求める式は数学的にきっちりした式です。）
しかし、
どれくらいの精度で議論できるかは
数字化した数に含まれる誤差がどれくらいの大きさかによります。
良い精度を出す技術は
机上の計算で済むものではありません。
場合場合に合わせて、
測った数字と付き合っていきたい
ものです。
＜追記＞2021.02.14
元の実体を使うのは
確実だと思う
「○○の解釈」「その５ 実数とは何か？」で考えたように
数字、実数の元の姿は
線分の長さなので、
実体そのもの（長さ相当の線分そのもの）を持ち運ぶのは
確実で理にかなっているのではないか
と思います。
道具を使って、賢そうに見えても、
実際の現実的には改悪ということも、ままあるのです。
（考え切れてなくて、浅知恵ということになるのですが。）
＜修正＞2021.02.14
数の原理を用いた説明で
参照しているのは
全て「その５ 実数とは何か？」でした
以上です。
＜追記２＞2022.01.27
DVDを見て
規矩術を知った
んですよ
最初は「石垣の積み方」に興味があって、
図書館にあったDVD
「日本古建築と伝統技法 第6巻 石垣修復の技術」を見たんですよ。
で、他の巻も見てみたら、
規矩術に関する巻（１，２，３巻）があって、
見たんですよね。
（一般に売って欲しいくらい、しっかりした内容に思えました。）
そうしたら、
実際に物を作れば、
測量で全部の長さを作れないことがわかることが
わかったのですが、
数学的な理論でも押さえておけば、
（原理的に押さえられるので。）
この大事な技術がとても大事だとわかるのではないかと、
記事にしてみたんですよね。
測量して、数値化することが
科学的アプローチ、科学的考察をするための第一歩で、
学校でも「測って数値化する」ことを
理科の科目を中心に習うのですが、
それでは「誤差付きの数値しか手に入らない」という事実があって、
（なので、科学的観察に関する議論に誤差ナシの議論はないんですよ。
機械で測るにせよ、人の目で測るにせよ、人のやることには誤差が必ずありますので。）
誤差ナシの長さを手に入れるにはどうするか
という
議論でもあるんです。
>
○○の解釈 > その７ 「量化する」との付き合い方
