> 根本の根 TOP> 21.平行光を作ろう
21.平行光を作ろう
平行光↓を作りたいんだけれど、どうしたらいいかな？
普通はどの光源も光る範囲に限りがあるから、
のようになって、
四方八方に広がる光、
つまり、お隣同士の光が平行ではないんだ。
（太陽も星の大きさがあるので、点光源だけれど、
十分遠いので、平行にものすごく近い。）
だから、平行光を作るとなると、
のように、
何か、人工的な「仕掛け」がいるね。
この「仕掛け」は光が通らないとならないので、
「ガラス」でできているとしてみよう。
両面が平行なガラスは、
良く知られているように、
斜め方向から来た光を同じ傾きの光で出すね。
こんな感じだ。
だから、両面が平行なガラス板は「仕掛け」として使えない。
でも、平行でないガラス板
ならどうだろう。
のようになるので、
どうやら光が曲がりそうだね。
光は同じ材質の物質の中を通るときはまっすぐ進むので、
肝心なのは、物質からの出入りのポイントなんだ。
そこに、どういう角度で入るかで、
出る角度が決まる。
平行でない２つの線同士を考えて、
三角形（正確には三角柱）のガラスで考えてみよう。
（とりあえず、２次元で考えるよ。）
１つの角度がθの直角三角形に
点光源から、入射角αで光が入ったとしよう。
で、実は、この角度で入ると、
この直角三角形では、出射角θで出てくるとしたいんだ。
これなら、図の直角三角形の底辺と平行に光が出てくるから。
逆に言うと、
底辺と平行に光が出てくる入射角がαということになる。
点光源との位置から、この場所でないと、
入射角はαにならない。
では、他の場所に入った他の点光源からの光は
きちんとこの光に平行に出てくるんだろうか？？？？
どうだろう？
ということで、
今の点よりも上の方で入射した光について考えてみよう。
この光は、下の図のように、
点光源からの角度として
α‘分だけ上に入っている。
（ただし、α‘>0。）
この光が
①（外側）、②（平行）③（内側）のどの線の光として出てくるかを
考えてみたい。
光が物質の境界面に入るときの角度と出ていくときの角度は
屈折率（２つの物質が何かによって決まる）で決まっていて、
しかも、角度そのものの関係ではなく、
sinの値としての関係になっているので、
絵をにらめっこしていても、よくわからないね。
なので、図に様々な変数と場所の記号をつけてみた。
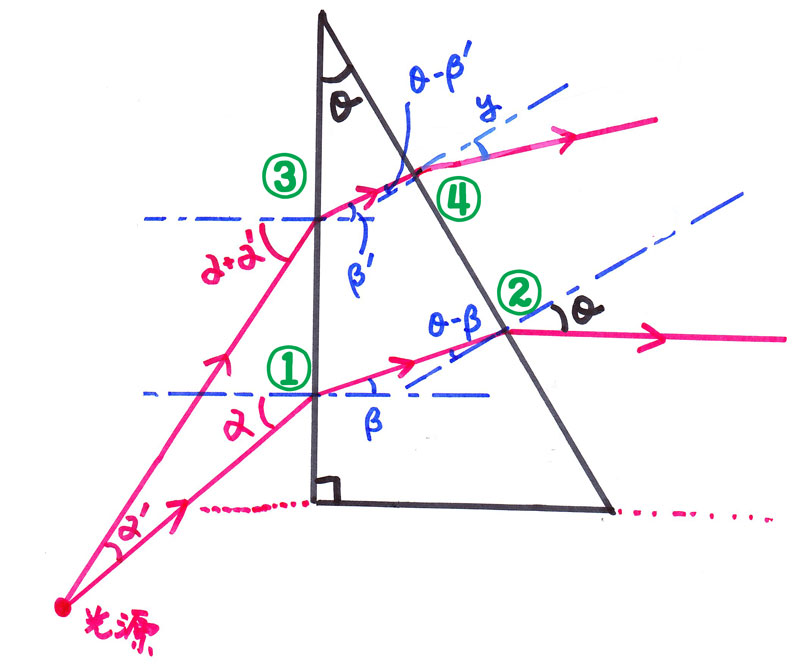
説明すると、
最初のモデルとなる底辺と平行になる光について、
①で入って、②で出ていく。
①の入射角をα、出射角をβとしよう。
そうすると、三角形の内角の関係から（自分で出してみよう）
②の入射角はθ-βとなる。
出射角はこの光の性質の定義からθだ。
比較対象のもう一つの光について、
③で入って、④で出ていく。
③の入射角は三角形の内角の関係から（自分で出してみよう）
α+α‘で
出射角をとりあえずβ‘としておこう。
そうすると、最初の光の時と同じように三角形の内角の関係から、
④の入射角はθ-β‘となるね。
で、出射角はわからないから、ｙとでもしておこうか。
いろいろな文字を置いたね。
ちゃんと光の筋が①②③のどれかわかるんだろうか？
（「ちゃんと文字に何か数字を入れてみた方がいいのではないか」と思った君、
いい感じだけれど、
今回は一般的な話のままで、
結論が出るんだ。）
場所①②③④でのスネルの法則に従った式を書いてみよう。
どうやって、θとyの大きさを比べたら良いだろうか。
θ=yなら、②で平行だね。
θ>yなら、①になって、光は外側へ行ってしまう。
θ<yなら③になって、光は内側へ行く。
同じ値だっていうし、
①の式と③の式を比べてみようか。
だそうだよ。
今回は知りたいことを知るために、
x=・・・みたいに解く必要はないんだ。
値の大小を比べたいだけだからね。
（等式を見たからと言って、解きたくなる必要はない。）
どうするかというと、
（右辺）の分子を見ると、
α‘>0だから、
α+α‘>α
だね。
ということは、
sinは90度までは角度が大きくなると、
sinの値も大きくなるので、
sin(α+α‘)>sin α
だね。
だけれども、
（右辺）の分数の値は（中辺）の分数の値と同じ
なんだそうな。
ということは、
（右辺）の分母も（中辺）の分母より
大きくないとおかしいね。
ということで、
sin β‘ >sin β
となる。
sinと角度の関係から、
β‘>β
だね。
とりあえず、一組考えたから、
もう一組
に行ってみよう。
さっきと同様に、
（自分で先は解いてみると良い。
今回は解答を書いておくけれど。
解き終わってから下へどうぞ。）
①と③の比較から、
β‘>β
だったから、
θ-β‘<θ-β
だよね。
ということは、
９０度までのsinと角度の関係から、
sin(θ-β‘)<sin(θ-β)
となる。
（右辺）の分母が（中辺）の分母より小さいのに
分数としての値が同じなんだそうな。
ということは、（右辺）の分母は小さくなるはずだね。
なので、
sin y < sin θ
となる。
９０度までのsinと角度の関係から、
y < θ
となるね。
ほら、大小関係なら出たでしょ？？？
（不等号は大小関係なので、「解けた」ともいう。）
一応、最後まで式の注釈をつけておこう。
となるよ。
２つの式をもう一度並べると、
ということで、
結局、
直角三角形の上の方に入った光は、
外側に行ってしまうことが分かった。
①になる。
ということは、
三角形ではだめそうだね。
つまり、
直線で構成された境界面では
平行線は作れないということなんだ。
じゃあ、どうしたら良いだろう？？
上の方にある光の出る場所の傾きを変えてみよう。
今度の目標は
y = θ
だ。
もう一度②と④の比較の式を出すと、
だね。
ということは、
分数の値を変えないで、
分子であるsin yの値
を大きくしないといけない。
（つまり、yを大きくしているから)
同時に
分母のsin(θ-β‘)の値を大きくする必要がある。
どうするかというと、
③の設定は変わっていないので、
β‘も変わらないから、
境界面の傾きであるθを大きくすればいいね。
と、境界面はθより寝ることになる。
光源から入る光の入射する位置が上になると、
垂直な方の面での出射角（③での出射角）が大きいがために、
傾きθでは足りず、もっと大きい角度が必要になるんだ。
逆に、
光源から入る光の入射する位置が下になると、
傾きθより小さい角度、
つまり、θより立つことになる。
仕掛けのガラスの形の傾向を図で表すと、
となるんだ。
つまり、連続した線で結ぶと、
のような凸型の曲線なら大丈夫そうだね。
２枚をくっつけることを考えよう。
にしたいんだけれど、
光源と中心（底辺に当たる場所）の高さをそろえた場合、
中心を通る光は直進してもらわないといけないので、
上下をくっつけたとき、
ここで垂直に面が立っていないといけない。
ので、
という形の傾向を持ったガラスが良さそうだね。
平凸レンズとして、良く知られているよ。
（虫眼鏡みたいに屈折を強くした両凸のレンズもあるよね。）
しかし、ずっと議論してきたように、
平のどの位置にどの角度で光が入射するかによって、
出てくる光が平行かどうかが決まっていたよね。
なので、
点光源の位置をレンズに対して
前後にずらしてしまうと、
一生懸命設計した予定が
（ここでは具体的な設計はしないけれど、
できそうでしょ？）
水の泡になってしまって、
平行光にはならない。
平行になる位置は
平らな面の手前には１か所しかなく、
焦点と言われる。
太陽光などの平行光を凸の方から入れると、
この焦点の場所で１か所に光が集まる。
虫眼鏡で太陽の光を集めると、
紙が燃えたりするよね。
（太陽光の当たる場所に虫眼鏡を
置いておいてはいけない。
燃えてしまうから。
気をつけよう。）
ということで、
「平行光を作ろう」
でした。
