> 根本の根 TOP> 4-2.図形的に言うと?
> 根本の根 TOP> 4-2.図形的に言うと?

4-2.図形的に言うと?
ズバリ、ヒントは同じ周の長さの長方形と正方形のどっちの面積が大きいか。
相加相乗平均とは
「2実数a 0、b
0、b 0に対して、
0に対して、
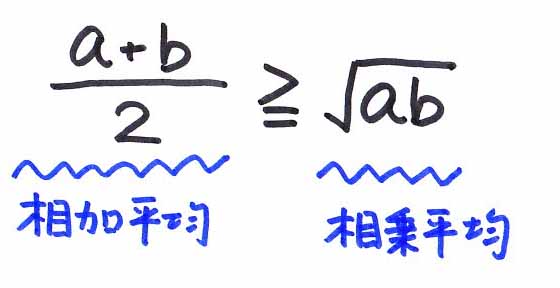
が成り立つ。」
という定理の名前だったね。
両辺を2倍しよう。
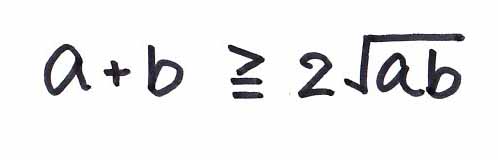
となるね。
こちらの式を証明しても、問題ないので、
こちらの式を使って、大小を比較しようと思う。
とりあえず話の流れを切りたくないので、
aまたはbの少なくともどちらか一方が0でない場合、・・・(*)
つまり、aもbも正の実数とするよ。
(数学の模範解答では(*)を先に書いてあるのだけれども、
メインの議論展開からはみ出した分について書いてあるので、
場合分けの根拠がわからず、模範解答を読みにくいと思う。
メインを先に読んで、
メインの議論展開の都合をわかった上で読むとわかりやすいし、
実際の解答ではメインの議論の後に場合分けで(*)を書いても大丈夫。
解答全体で議論の対象となるすべての場合を考えつくされているから。)
2辺の長さが、a、bの四角形の面積と縦横の辺の長さの和について考えよう。
(左辺)が縦と横の辺の長さの和で、
(右辺)が同じ面積の正方形の時の縦と横の長さの和だ。
どっちが大きいんだろう。
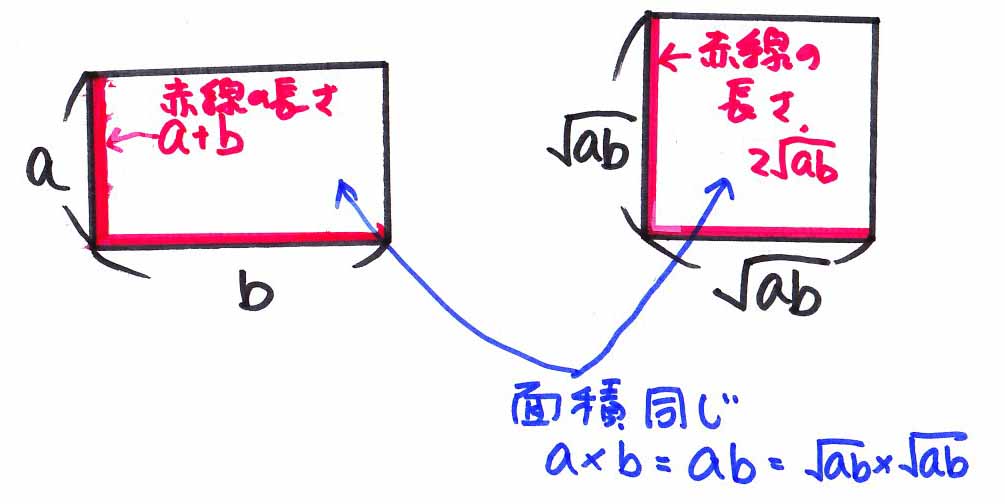
結論から言うと、同じ周の長さだと、実は正方形の方が長方形よりも面積が大きいんだ。
(要証明:1本の棒を折り曲げて長方形を作るときにいつ面積が最大になるかという二次関数の例題)
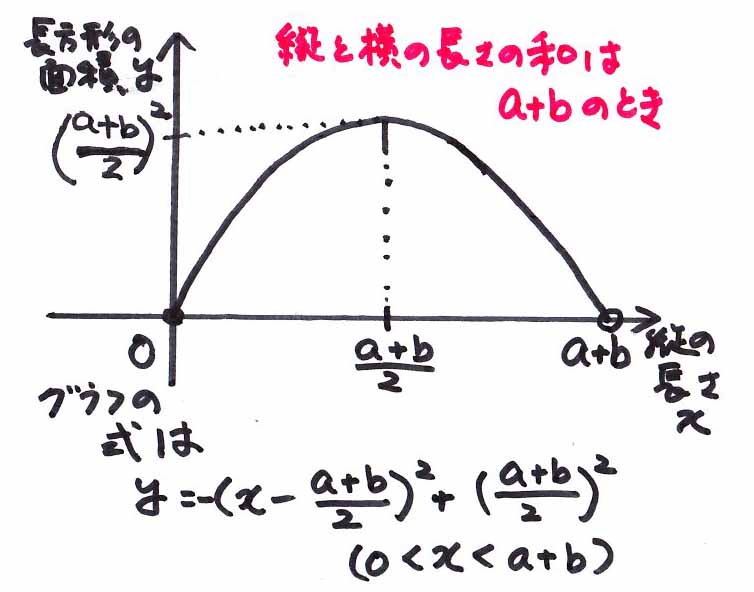
ということは、同じ面積とすると、長方形の方が正方形よりも周の長さが大きくなる。
縦と横の長さの和は面積同じで正方形にしてしまった場合よりも長くなる。
そして、たまたまa、bの長さが同じとき、つまり正方形について考えると、
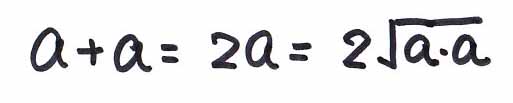
というように、等しくなるんだ。
さて、まだ考え残していることがあったね。
aまたはbの少なくとも一方が0である場合。
今回は実際にこの世に存在する面積と長さという概念を使って、
メインを料理したので、
図を描く関係上辺の長さが0という場合をとりあえず外して考えた。
でもそれでは、最初のお題の
「2実数a 0、b
0、b 0に対して、」
0に対して、」
という条件をすべて考えたことにならない。
そこで、残りを考えよう。
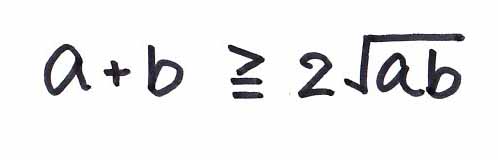
の式に関して、
aもbも0ならば、両辺が0なので、等号が成り立つ。
aまたはbが0ならば、(左辺)は正の数で、(右辺)は0。
よって不等号>が成立。
よって、
「2実数a 0、b
0、b 0に対して、」
0に対して、」
検討が済んだので、完全に証明が終了になる。
できたのであれば、「できたよー」と旗を立てて宣伝しないといけないので、
以上より(この文言の上の議論全てを引いてます)
「2実数a 0、b
0、b 0に対して、
0に対して、

が成り立つ。」
が証明された。
と書かないといけない。
短く書きたいときには、
「以上より題意が証明された。」
みたいに書くよね。
結局、相加相乗平均の式は正方形と長方形の辺の長さの和と面積に関する式だったんだ。
この解き方は数学の式としては、
最善手と言われるような手数の少ない美しい解き方ではないかもしれない。
しかし、どういう意味のある式なのかを考えるという解析的な手法で式を分析することは
式の理解の上で必要なんだ。


 > 根本の根 TOP> 4-2.図形的に言うと?
> 根本の根 TOP> 4-2.図形的に言うと?

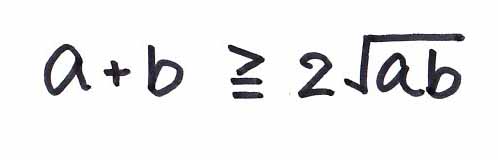


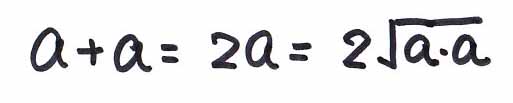
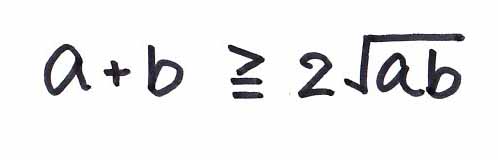

 > 根本の根 TOP> 4-2.図形的に言うと?
> 根本の根 TOP> 4-2.図形的に言うと?