> 根本の根 TOP> 流体力学におけるオイラー記述の適応条件についての1意見
> 根本の根 TOP> 流体力学におけるオイラー記述の適応条件についての1意見
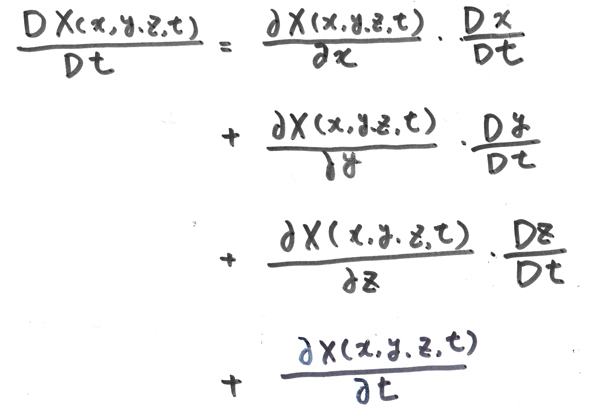 ...(*1)
...(*1)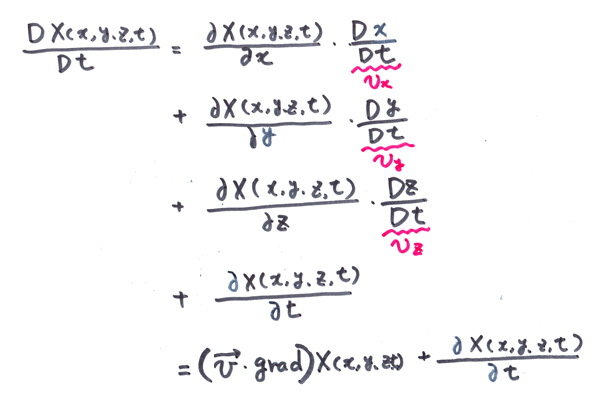 ...(*2)
...(*2)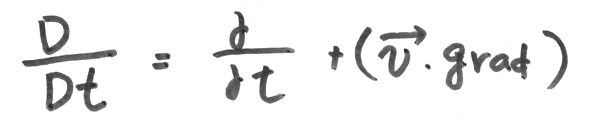 ...(*3)
...(*3) ...(*4)
...(*4)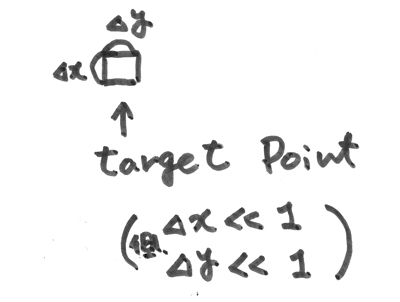 という観測領域を設定し、
という観測領域を設定し、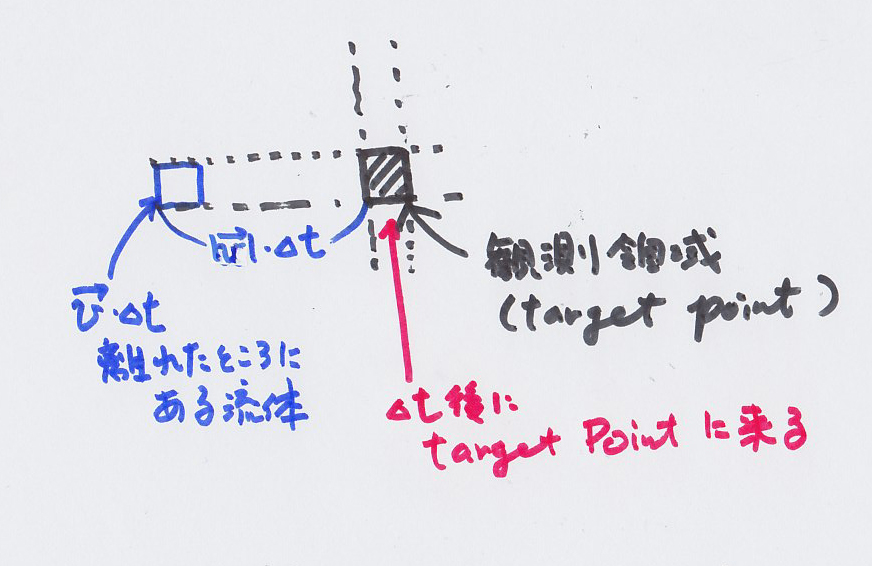
 離れた場所にあった流体です。
離れた場所にあった流体です。 離れた場所にあった流体で、
離れた場所にあった流体で、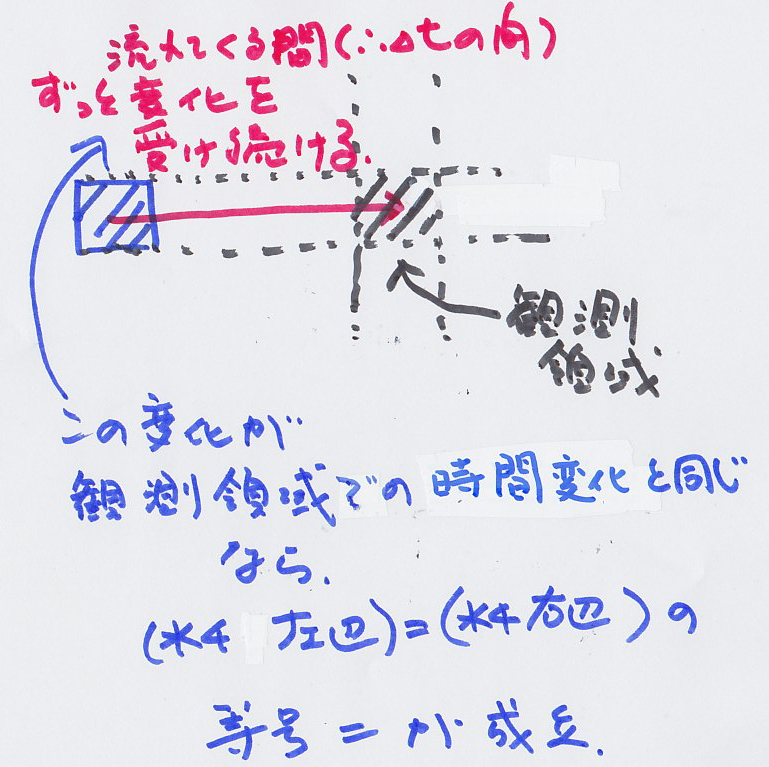
 の適応される
の適応される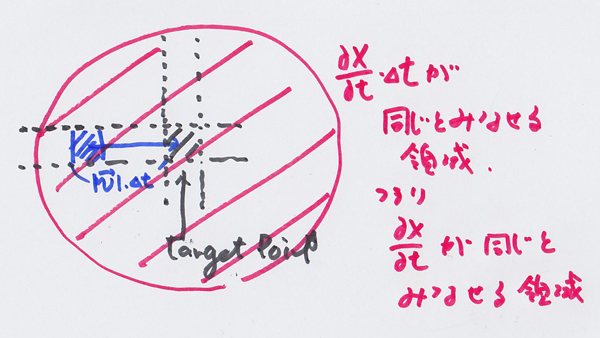
 の均一な領域はΔtを小さくすれば、
の均一な領域はΔtを小さくすれば、 の距離はΔt→0とすることで、
の距離はΔt→0とすることで、 離れた位置にあった流体であると
離れた位置にあった流体であると
 という観測領域を設定し、
という観測領域を設定し、
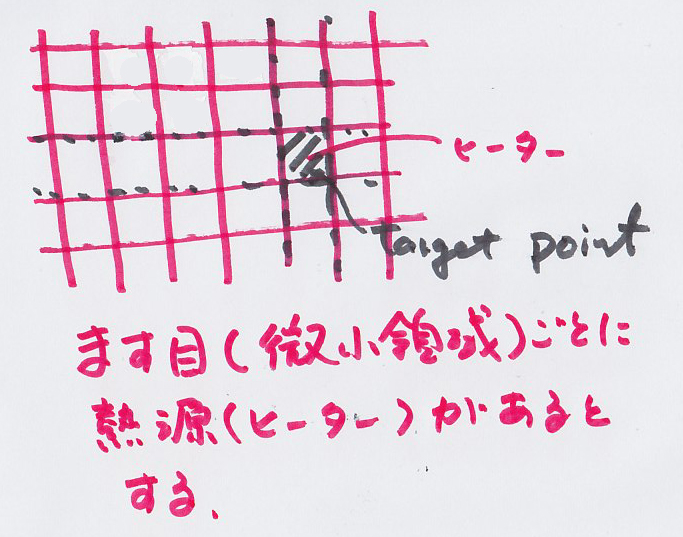
 ...(*5)
...(*5)
 離れた2点間の温度差です。
離れた2点間の温度差です。 離れた流体が流れてくる間の同時刻のΔtの間、
離れた流体が流れてくる間の同時刻のΔtの間、 離れた流体が流れてくる間の同時刻のΔtの間、
離れた流体が流れてくる間の同時刻のΔtの間、 離れた流体が温められた分」ではありません。
離れた流体が温められた分」ではありません。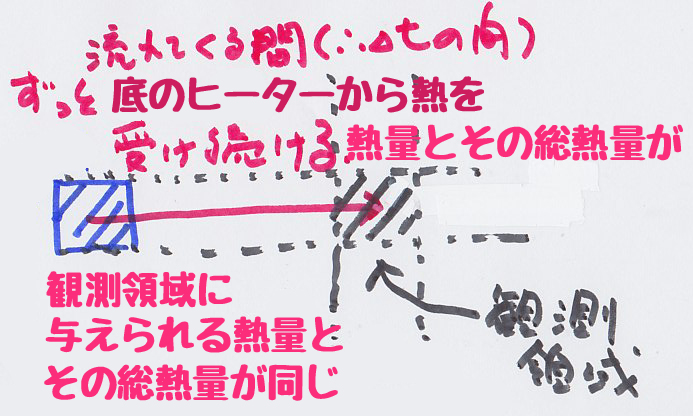
 離れた場所にあった流体であると
離れた場所にあった流体であると の距離で、
の距離で、 の距離はΔt→0とすることで、
の距離はΔt→0とすることで、
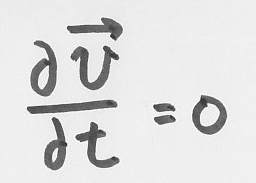 としないと、
としないと、 > 根本の根 TOP> 1.流体力学におけるオイラー記述の適応条件についての1意見
> 根本の根 TOP> 1.流体力学におけるオイラー記述の適応条件についての1意見